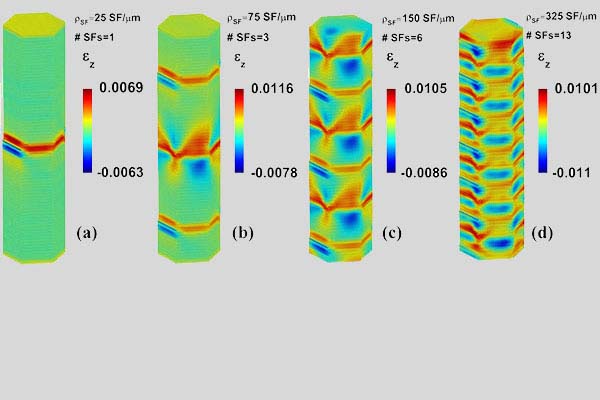
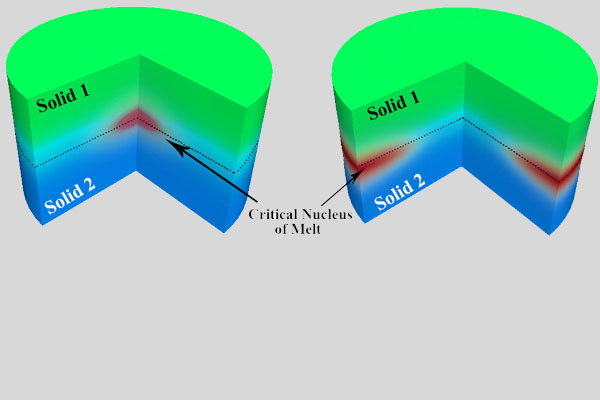
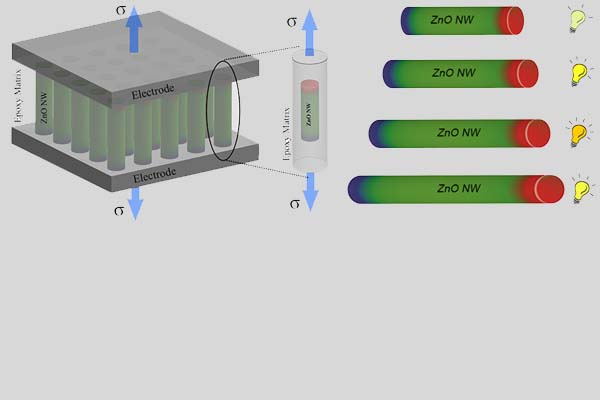
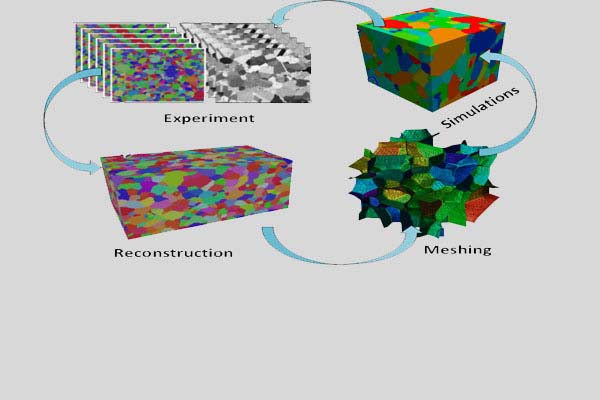
Research Overview
We are interested in understanding atomic and molecular processes, developing mathematical and numerical models, and establishing computational tools for multiscale/physics systems with the aim of hierarchical design of advanced and nanomaterials. To achieve this goal we utilize atomistic simulations, mesoscale modeling techniques, and higher scale continuum models in close collaborations with experimental researchers worldwide to unravel the materials genome and design materials with superior properties. We are focused on the following areas:
- Materials under extreme environments
- Energetic materials
- Materials for energy
- Low-Dimensional Materials
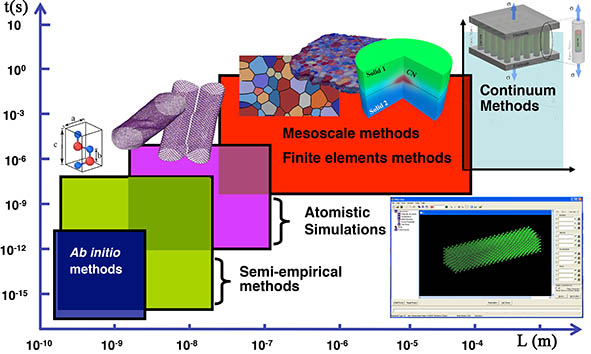
The thorough understanding of each of these research directions involves multiple scales. Although here we have employed multiscale techniques in most cases to investigate the materials response, the results are presented based on each individual scale to simplify their presentation. Details of our research on each of the above areas are elaborated in the section associated with the technique used for the corresponding study, e.g., atomistic research. There are multiple occasions that different terms are utilized for describing the same method which may cause confusion. Here different terms utilized throughout our study are briefly described to avoid any misinterpretations.
What is a Theory?
A theory is a set of logically or mathematically interrelated principles and definitions, which determines the relations between a set of variables, and serves the purpose of explaining a natural phenomenon. (F.N. Kerlinger 1986; D. Jary & J. Jary 1995)
As the number of successfully tested situations for a theory increases and covers a wider range of diverse conditions, the developed theory becomes more famous and respected. For an analytical framework to become a theory, applicability to situations other than those used during the development stage is necessary; otherwise, it's just a data fit rather than a theory.
Modeling vs. Simulation
In the process of studying any system, theoretically, experimentally, or through simulations, a series of inputs (controls) will be manipulated and the system response measured through a set of outputs (observables). The goal of theoretical work is to find a relation between outputs and inputs. The main purpose of this process is decoupling interactions and removing those with minor impact. Therefore, a model is simpler than the system and has a smaller number of degrees of freedom. In contrast, a simulation is more complex than the real system and accesses a larger number of states, imposing constraints to mimic the behavior of the real system. (Casti, 1989)
What is Multiscale Modeling?
Multiscale modeling is a field of science that studies physical systems and phenomena with important features spanned along multiple length and time scales, often involving multiple physical phenomena. Numerous multiscale methods tackle scaling problems in mechanics and materials science, especially systems with nanometric dimensions, such as quasi-continuum, ab-initio molecular dynamics, and coarse-grained molecular dynamics.
Multiscale modeling techniques open new opportunities for academic research and industry. They reduce production costs by reducing production time and the number of expensive experimental tests, optimizing design, process, and material; and increasing quality and performance. Meanwhile, they bring new challenges, including bridging between different scales, computational bottlenecks, and capturing multiphysics phenomena. (Horstemeyer, 2009)
What is Multiscale Simulation?
These are a class of simulations that capture the behavior of systems and materials along multiple length and time scales and can be classified into two main categories: hierarchical and concurrent approaches. In the hierarchical approach, simulations are performed at different scales, and information from lower scales is extracted using a bridging methodology (e.g., statistical mechanics and homogenization techniques) and passed to the higher scale. Therefore, multiscale simulation occurs through multiple stages, each dealing with only a specific length and time scale. Concurrent methods, on the other hand, use specific numerical techniques and computational algorithms to transfer information between different scales on the fly.
What is an Experiment?
Oftentimes, in the literature, the term 'experimental work' signifies any laboratory/field-related activity. A significant part of this activity is devoted to designing experimental methods for measuring physical parameters and features, which may involve designing new equipment. Part of any experiment is quantifying the data, involving direct measurements of physical quantities (e.g., elastic modulus, piezoelectric constant, and yield strength) under various conditions (e.g., corrosive environment, high vacuum, and zero gravity). However, in the classical experimentalist's context, a difference is made between 'experiment' and 'measurement'. In this context, calculating a known material property is classified as a measurement rather than an experiment.
An experiment attempts to resolve a broad question through suitable choosing of laboratory/field conditions to investigate/establish a connection among multiple physical potential parameters. Although an experiment commonly involves a series of measurements to set up or explain a new concept, a sequence of measurements is not necessarily an experiment. Experiments may test an idea and answer a simple question, or they may be the outcome of analytical development and testify to seemingly contradictory results. (W.G. Knauss, 2000)
"...all too often, experimental work in applied mechanics is thought of only as a check on existing theory or as a convenient substitute for analysis. This is a valid but rather inferior function of experiment. The greater and essential contribution is to guide the development of theory by providing the fundamental basis for an understanding of the real world." - Drucker (1967)